Misure sugli amplificatori in classe D

di Michele Viola

Le misure sugli amplificatori, in classe A o B o D che sia, riguardano gli stessi parametri di qualità: l’audio è audio, insomma. La distorsione o il rumore spurio che non vorremmo ascoltare hanno uguale importanza indipendentemente dalla tipologia specifica del dispositivo.

Per poter caratterizzare un amplificatore in classe D è però necessaria una notevole elaborazione. In particolare occorre demodulare il segnale PWM (Pulse Width Modulation) presente all’uscita dello stesso.

Qualche tempo fa, per motivi che possiamo definire didattici, mi è capitato di avere a che fare con un problema di questo tipo.

Supponiamo, ad esempio, di voler determinare la risposta in frequenza di un amplificatore di potenza, in modulo e in fase; a questo fine è sufficiente portare all’ingresso dell’ampli un segnale sinusoidale: il segnale in uscita da un amplificatore lineare sarà anch’esso più o meno sinusoidale (a meno della distorsione, ma questo è un altro problema). Il modulo della funzione di trasferimento si può determinare ad esempio come rapporto dei valori di cresta delle due sinusoidi, mentre la differenza tra le fasi si può stimare confrontando i passaggi per lo zero. Il segnale che esce da un amplificatore in classe D non è però sinusoidale neppure in prima approssimazione ma PWM; questo significa che il valore di cresta coincide, più o meno, con il limite dell’alimentazione indipendentemente dall’ampiezza della sinusoide mentre il passaggio per lo zero avviene in media qualche centinaio di migliaia di volte al secondo e non ha niente a che fare con la fase della sinusoide.

Il segnale PWM in uscita, naturalmente, contiene informazioni sufficienti per ricostruire la sinusoide corrispondente al segnale d’ingresso (altrimenti cosa ascoltiamo?), solo che queste informazioni sono nascoste dalla modulazione a larghezza d’impulso. Per individuare la sinusoide si può fare la stessa cosa che farebbe un altoparlante o lo stesso sistema uditivo: un filtraggio passa-basso di caratteristiche opportune.

Occorre notare che un filtro passa-basso è di norma già presente tra l’uscita dell’amplificatore e il carico. Tipicamente si tratta di un filtro LC del secondo ordine, anche se può essere molto più (o molto meno) complesso. Questo però non è sempre vero, nel senso che esistono in commercio amplificatori in classe D (per lo più di piccola potenza) privi del filtro d’uscita, progettati per delegare totalmente al carico la funzione di filtraggio. Il filtro d’uscita, inoltre, ha lo scopo di attenuare l’energia ad alta frequenza, ma sarà solitamente ben lontano dall’offrire un segnale completamente “ripulito” dalle componenti spettrali al di fuori dalla banda audio, perché parte della funzione di filtraggio può essere tranquillamente svolta da un carico induttivo (come un altoparlante) ed eventuali residui non verrebbero comunque raccolti dal sistema uditivo umano. Il filtro d’uscita è spesso la parte più impegnativa nella realizzazione di un amplificatore audio PWM, sia dal punto di vista del costo (anche 1/3 dell’intero costo del dispositivo), sia dal punto di vista delle dimensioni e del peso. Ultimo, ma non ultimo, in fase di progetto e di prototipizzazione può essere molto utile osservare l’uscita del dispositivo a monte dell’eventuale filtro d’uscita, anche al fine di dimensionare correttamente il filtro stesso.

Il filtraggio digitale

Una via possibile per la visualizzazione della forma d’onda in banda base contenuta nel segnale modulato PWM è l’elaborazione digitale. In pratica, una volta campionato il segnale PWM “così com’è”, lo si può elaborare tramite un filtro digitale per ottenere lo stesso risultato che si otterrebbe utilizzando un filtro analogico prima dell’acquisizione.

L’acquisizione va fatta con uno strumento adeguato, come un oscilloscopio a campionamento di adeguati banda passante e sample rate.

Il problema dell’oscilloscopio a campionamento è che si tratta generalmente di uno strumento a bassa risoluzione, anche se spesso molto veloce (almeno per i modelli più sofisticati). Il trade-off tra velocità di campionamento e risoluzione è ovviamente dettato da ragioni fisiche e tecnologiche, per cui riguarda tutti i dispositivi di acquisizione e non solamente gli oscilloscopi. La scarsa risoluzione contro la velocità di acquisizione potrebbe però non essere un problema per quanto riguarda la misura di un segnale PWM. Diciamo che, come al solito, dipende dalle informazioni che intendiamo estrarre dalla misura. Un segnale PWM ideale ha un’ampiezza di picco costante (uguale in pratica ai limiti dell’alimentazione o, al limite, al doppio nel caso di dispositivi a doppio ponte), quindi l’informazione contenuta nell’ampiezza è in teoria solo una costante di proporzionalità. Il contenuto informativo è interamente contenuto nel duty-cycle, che può essere misurato rilevando i tempi di permanenza su ciascun livello (alto o basso, o al limite anche sullo zero per alcuni tipi di finali a doppio ponte).

Il filtro a pettine

Lasciando perdere, per il momento, FIR e IIR, il modo più semplice e più rapido dal punto di vista computazionale per realizzare un filtraggio passa-basso digitale è quello di implementare il calcolo di una media mobile, non pesata, di periodo pari all’inverso della frequenza da eliminare. In pratica, la funzione di trasferimento equivalente di un filtro siffatto presenta un andamento di tipo sin(x)/x, con gli zeri in corrispondenza dei multipli interi dell’inverso del periodo di integrazione.

Questo tipo di filtraggio può influire però anche sulla misura dell’ampiezza in banda passante, e sarebbe necessario stimare l’entità dell’errore introdotto.

Risparmiando, in questa sede, i calcoli, peraltro non eccessivamente complessi, diciamo che, nel caso di un segnale sinusoidale, l’errore commesso considerando il risultato della media al posto del vero valore massimo della cosinusoide è inferiore a 0,1 dB quando la prima armonica da eliminare è uguale o superiore a 250 kHz.

Non mi sono qui posto il problema se fosse possibile contenere ulteriormente l’errore utilizzando un insieme di coefficienti di pesatura adeguati per i campioni da mediare, eventualmente con un poco di impegno in più dal punto di vista computazionale. Questo tipo di argomentazione è trattato estensivamente nella teoria dei filtri digitali a risposta finita, detti anche “filtri FIR”.

Il campionamento del segnale PWM

Per osservare il segnale PWM e campionarlo al fine di una successiva elaborazione ho usato un oscilloscopio a campionamento collegato con un canale all’ingresso ed uno all’uscita di un piccolo amplificatore in classe D, del tipo che viene di solito inserito in dispositivi come computer portatili e simili. Ho cercato di catturare circa due periodi alla massima risoluzione: l’oscilloscopio che ho avuto la possibilità di utilizzare mi ha concesso 1.250.000 campioni per canale con un periodo di campionamento di 1,6 ns.

Il segnale presente in uscita in queste condizioni è rappresentato nella figura 1.

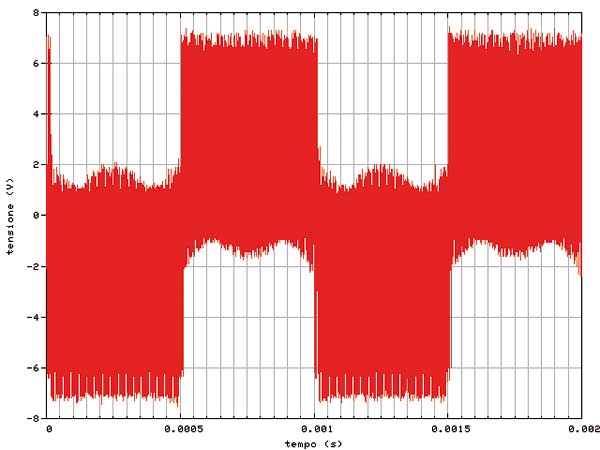
Come ci si poteva aspettare, non è certamente possibile riconoscere alcuna sinusoide nel segnale d’uscita così com’è. Con un po’ di fantasia si può forse intuire la fase ma non è possibile, ad esempio, neppure una stima approssimativa dell’ampiezza.

Nella figura 2 ci sono 50 µs di segnale tratti dallo stesso file, da cui si può vedere con maggiore precisione la forma degli impulsi.

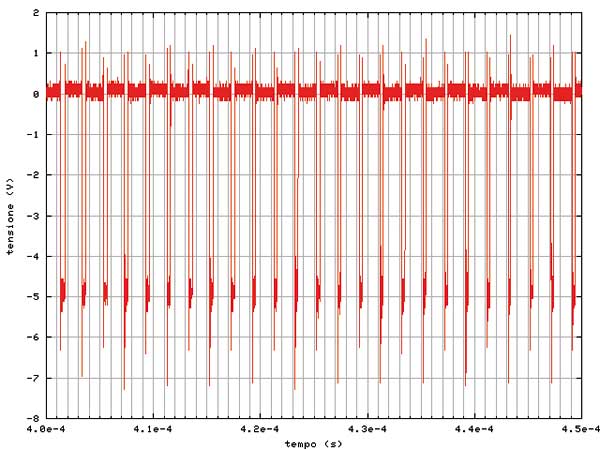
L’elaborazione digitale

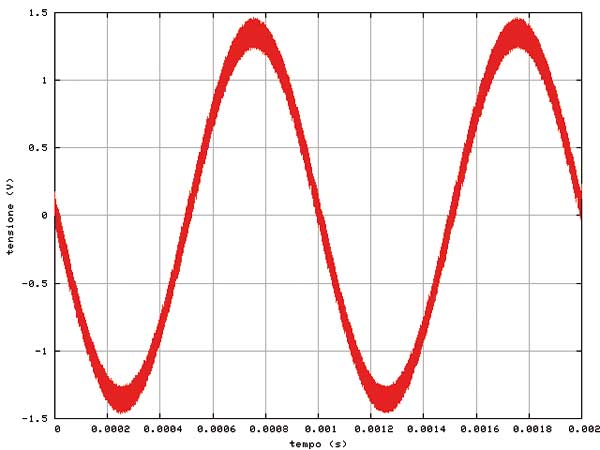
Come si nota immediatamente dalla figura 3, dopo il filtraggio il segnale è decisamente più comprensibile. L’amplificatore evidentemente inverte, cioè sfasa il segnale di 180º. Il valore di picco, rilevato dalla figura, è approssimativamente di 1,35 V e confrontato con gli 0,5 V in ingresso (almeno secondo il quadrante del generatore di segnale), lascia dedurre un guadagno di circa 8,6 dB, rispetto agli 8 dB nominali del piccolo amplificatore in esame. Queste sono solo considerazioni espresse al fine di verificare la validità del ragionamento. Ovviamente è possibile dare maggiore consistenza a questi numeri analizzando con maggiore precisione i dati ricavati. Un secondo passaggio del filtro digitale, che si è agganciato questa volta intorno ai 250 kHz (rispetto ai 500 kHz del primo) rivela una forma d’onda decisamente più pulita, di cui un estratto è visibile in figura 4.

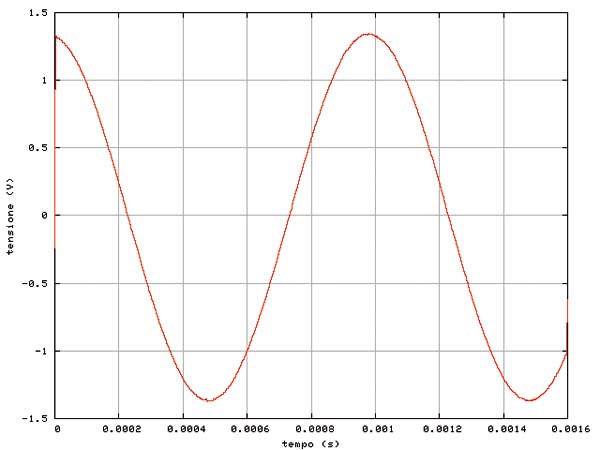
Occorre anche specificare che il presente scritto non vuole oltrepassare il significato appunto didattico che ne ha guidato l’esperienza alla base. Esistono, già da qualche tempo, strumenti di misura in grado di eseguire egregiamente tutti i passaggi necessari per caratterizzare dal punto di vista metrologico gli amplificatori in classe D. Spero qui, semplicemente, di essere riuscito a dare un’idea di alcune delle problematiche da risolvere, in maniera più o meno automatica, per ricavare, da un amplificatore di potenza in classe D, anche solamente il guadagno a 1 kHz.