Che Patacca!

di Stefano Cantadori

Il private equity formato da Kohlberg Kravis Roberts & Co. e Goldman Sachs Group Inc., cioè l’annunciato compratore del gruppo Harman, ha cambiato idea all’ultimo minuto. L’acquisto non si è perfezionato.

Ho telefonato a Gianni per vedere se insieme potevamo fare il colpo grosso: “Vecchio mio, non avresti 8 bilioni di dollari fino a martedì?”. Mi ha dato, giustamente, del patacca.

Trovate maggiori info, in inglese naturalmente, sul numero di ottobre di FOH (www.fohonline.com). Ci sono stati nel frattempo ulteriori sviluppi? Chissà.

Oggi studiamo: “Come cala la pressione quando ci allontaniamo dalla sorgente”.

Introdurremo inoltre i concetti di Intensità e di Potenza Sonora, roba che scotta. Vi piacerà.

Tutti sanno che per un line array, la pressione cala di 3 dB ogni raddoppio della distanza e non di 6 dB come invece avviene per le sorgenti semplici. Perché? Sarebbe facile rispondere ma io vi complico la faccenda.

Cercheremo anche di capire perché, nel cosiddetto campo lontano, la pressione torna a calare di 6 dB anche se la sorgente è un line array. Pure in questo caso potrei arrivare alla spiegazione in modo diretto ma preferisco procedere a zig zag.

Evitando le formule, insomma.

Facciamo le luci

Per prima cosa procuratevi una torcia elettrica e una stanza buia o quasi. Siamo nello show biz e le luci contano più dell’audio, fatevene una ragione. Impugnate solidamente la torcia per il manico. Ora calatevi le brache (no, non fatelo, sto scherzando).

Puntata la lampada contro il muro, girate la ghiera davanti alla torcia per allargare o stringere il fascio. Vedrete che più si allarga il fascio, meno intensa sarà la luce sul muro. Se regolate la ghiera per un fascio divergente a piacere e vi allontanate dalla parete, noterete che l’intensità diminuisce poiché la superficie illuminata cresce.

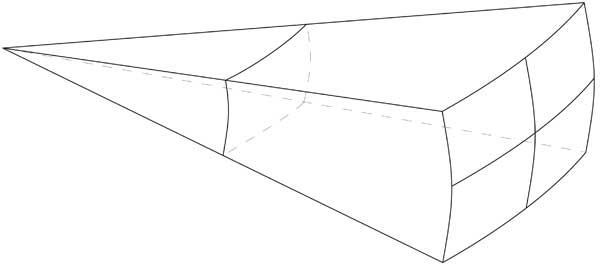
Costruitevi con del filo di ferro lo strano meccanismo in figura 1 (no, non fatelo, è sufficiente guardare la figura). Noterete certamente che a distanza x dalla sorgente la luce si dispone su una superficie unitaria, a due volte la distanza x la luce illumina una superficie 4 volte maggiore, a tre volte la distanza la superficie è 9 volte maggiore, a quattro volte la distanza la superficie illuminata è 16 volte.

Possiamo perciò anche dire che l’intensità della luce ricevuta nel primo caso, quello della superficie unitaria, è quattro volte superiore che nel secondo e sedici volte superiore rispetto alla distanza quadrupla. Quadruplica per ogni dimezzamento della distanza.

... Intensità?

Intensità sonora

Prendiamo, e ti pareva, la solita sorgente puntiforme e facciamo scoccare la nostra scintilla.

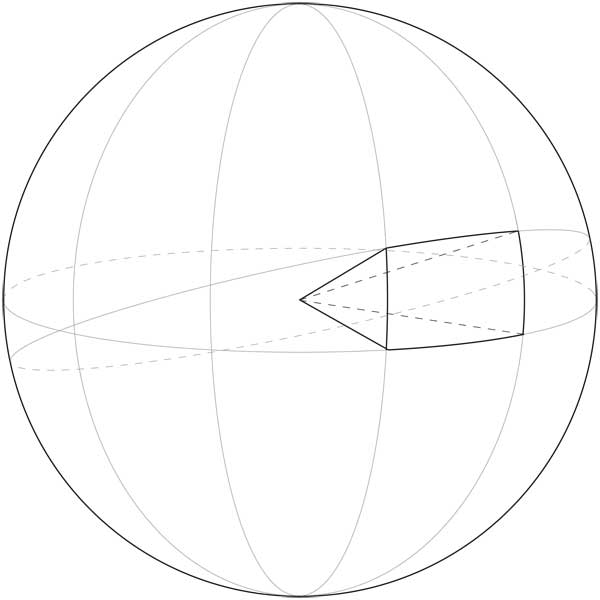
Il suono si allontana dalla sorgente e, come solito, andrà ad illuminare uniformemente la superficie di una sfera. Più passa il tempo più il suono si allontana dalla sorgente e più sarà grande la superficie della sfera illuminata. Come sempre.

L’intensità acustica, come intuibile dagli esempi di cui sopra, è l’energia che nell’unità di tempo attraversa una superficie¹.

Se immettiamo il marchingegno nella “sfera”, avremo una rappresentazione grafica piuttosto intuitiva.

Di palo in frasca ma non troppo: faccio notare che il filamento della lampadina è reso direttivo dalla parabola, altrimenti farebbe luce in ogni direzione… se metto una sorgente (acustica) puntiforme nel fuoco di una parabola, mirabilia, ottengo un fascio stretto come non mai (se la parabola è grossa abbastanza per le frequenze di cui mi interesso).

Un momento di pausa. Ti offrirei un caffè ma sono giù di mano.

Sarebbe utile ricordare quello che abbiamo studiato in precedenza ma qualche richiamino lo faccio comunque.

Dall’articolo sui decibel (S&L n. 60) ricorderemo che quando un’intensità raddoppia, l’incremento è di 3 dB. Quando raddoppia una pressione l’incremento è invece di 6 dB.

Confiniamo intensità e potenza

Componiamo ora una tabella per vedere come si comportano queste grandezze – Pressione, Intensità e Potenza – quando la nostra sorgente semplice irradia in spazi confinati (rispetto a quando irradia senza ostacoli in modo sferico).

Nel numero 59 avevamo scatenato un putiferio limitandoci ad osservare la pressione. Riporto qui i disegni di allora, con l’aggiunta di una tabellina.

È evidentissimo che al dimezzare dello spazio di irradiazione l’intensità quadruplica, come da esempio grafico. La pressione raddoppia per le ragioni già illustrate a suo tempo (sorgente immagine). È per questo che entrambe le grandezze salgono di 6 dB (o diminuiscono di altrettanto se raddoppio lo spazio).

L’una quadruplica, quindi +6; l’altra raddoppia, quindi +6. (S&L n. 60)

Con questo, cosa voglio dire?

Che sulla superficie di un fronte d’onda sferico generato da una sorgente semplice, misurerò ovunque la stessa pressione, generata da onde di compressione/rarefazione che arrivano in fase e senza interferenze (e con cosa potrebbe interferire? La sorgente è una sola e non ci sono riflessioni).

Tale pressione, per le ragioni che abbiamo visto aggirandoci dalle parti dell’intensità, ad ogni raddoppio della distanza diminuirà di 6 dB SPL. Il tutto in campo libero, naturalmente.

Line array composto da sorgenti semplici

Invece di una sola sorgente semplice ne consideriamo parecchie e in fila indiana.

Nel numero precedente avevamo creato sperimentalmente un fronte d’onda “piatto” gettando in acqua una fila di sferette² per simulare un line array costituito da sorgenti semplici.

Se disponiamo in campo libero una colonna di sorgenti semplici, il fronte d’onda somiglierà a un cilindro, leggermente panciuto poiché il troppo “piatto” stroppia.

Se guardo la sorgente lineare dal punto dal punto di vista dell’intensità? Ecco cosa succede alle superfici illuminate ogni raddoppio della distanza³

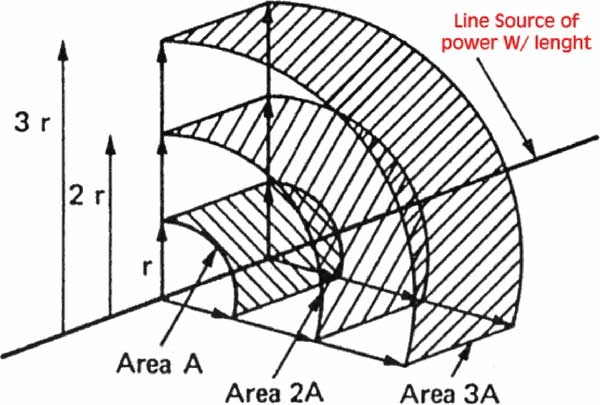
Intuitiva, ancora una volta, la relazione con la pressione. Al raddoppio della distanza, infatti, la superficie illuminata raddoppia invece che quadruplicare come nella propagazione sferica. Per cui I diminuisce di soli 3 dB e SPL pure. Un decremento di 3 dB SPL = 0,7065 volte .

Perché ho messo il termine “piatto” fra virgolette? Piatto è una parola grossa e, come menzionato in passato, ricordo al lettore che un fronte d’onda piatto ha attenuazione zero e propagazione infinita. Non esiste in natura ma è citato con sicurezza come caratteristica dell’impianto x o y da parecchi uffici marketing. Anche io ogni tanto commetto, per comodità di discorso, lo stesso errore e faccio ammenda. Reperita juvant (il latino fa sempre figo).

Altri punti di vista

Come già visto in altri numeri della rivista, le sorgenti fra loro interferiscono dando luogo nel line array ad un lobo principale lungo l’asse mediano e ad altri lobi secondari con minore energia. Più mi allontano, più il mio fonometro (che come le mie orecchie legge la pressione e non il fronte d’onda) coglierà lungo l’asse del lobo il contributo di via via più sorgenti; di questo abbiamo parlato più diffusamente in passato. Se esco dal piano verticale del line array, cioè dal lobo principale, la pressione cade violentemente.

La sorgenti in colonna non fanno altro che creare una sorgente direttiva sul piano verticale (quello dell’asse su cui sono allineate le sorgenti).

L’energia è convogliata e ristretta in una porzione di spazio, possiamo dire confinata, per cui in quella direzione ne misurerò di più che non se la propagazione, a parità di energia emessa dal motore, fosse sferica.

Come nell’esempio della lampadina con la parabola, del driver con la tromba, dello spazio confinato.

Insomma, quanto cala la pressione?

Dipende dalla sorgente, dal mezzo in cui il suono è trasmesso e dalle condizioni al contorno. Non fidatevi. Siate cauti. Fatti non foste per viver come bruti ma per seguir virtute e canoscenza⁴.

Dipende anche dalla forma della sorgente. Un J array mica è un line array. È un line array solo nella parte dritta della stanghetta.

Abbiamo già studiato gli effetti di rifrazione, per cui interi quartieri vicini ad una fabbrica rumorosa vengono “saltati” dal rumore che va ad appestare zone ben più lontane. E di come i nostri concerti talvolta non si sentono in piazza ma al quinto piano sì.

In un palasport o in un capannone industriale, ad esempio, il suono diretto si combina con il campo riverberato dando luogo ad un incremento locale (i due suoni non sono correlati ed in fase per cui l’incremento di pressione è di soli 3 dB). Oltre quella zona la pressione del campo riverberato generato da un suono stazionario risulta pressoché omogenea in tutto l’ambiente⁵. La propagazione sonora incontra riflessioni, assorbimenti, ostacoli, cazzamaveri che accumulano energia e la rilasciano nel tempo o la sottraggono. La realtà spesso può creare forti deviazioni dallo “sperato”.

Va quindi sempre usata cautela quando nella pratica si applica la regola dei 6 dB di attenuazione per una sorgente puntiforme (la maggior parte delle sorgenti che ci circondano si propagano per onde pressoché sferiche e si comporta così) e quella dei 3 dB per i line array. Una fabbrica, in genere, si comporta a distanza come una sorgente concentrata, strade trafficate e ferrovie vengono invece viste come sorgenti lineari.

Quando si è nel campo vicino di un array non tutti i suoni emessi da tutti i punti dell’array si sono combinati insieme. Anzi, quella famosa distanza detta “far field” per un line array è proprio quella dove l’attenuazione comincia ad essere quella di una propagazione sferica. Per n sorgenti in array viste da molto lontano, il fronte d’onda torna ad essere sferico.

Più corto l’array, più vicino sarà il campo lontano. Freddura.⁶

Dei line array sapevate già tutto e anche di più. Spero, come sempre, di aver gettato luce su qualche ombra ed aver suscitato qualche dubbio.

Tutte scuse per infilare nel discorso Intensità e Potenza sonora, che mi scottavano in mano già dal terzo articolo di questa serie.

La prossima volta, vedremo.

Note:

1. L’intensità I è la media nel tempo dell’energia trasmessa attraverso un’area unitaria perpendicolare alla direzione di propagazione, e si misura in W/m².

La potenza acustica si ottiene moltiplicando la componente normale (o perpendicolare che dir si voglia) dell’intensità per la superficie che racchiude la sorgente.

La pressione, come avevamo già visto in precedenza, è l’energia che passa in un punto e si misura in dB SPL

2. L’esperienza del plucciatore lineare ad L è di Frank Fay (tratta da “Foundations of Engineering Acoustics”).

3. La figura è tratta da una dispensa di Paolo Medici.

4. Cfr: Roberto Benigni.

5. Non è il vostro impianto ad essere responsabile di una copertura così omogenea. Vi piacerebbe eh?

6. Somiglia a quella dell’albero Ontano. Che è quell’albero che pur essendo vicino è sempre l’Ontano.