Ancora setacci

di Stefano Cantadori

Ci siamo già diretti verso la zona dei filtri, nei numeri 88 e 89, occupandoci di alcuni aspetti poco conosciuti. Se dovessimo filtrare la sabbia da un terreno che contiene ghiaia e sabbia, non dovremmo preoccuparci delle relazioni di fase che ghiaia e sabbia potrebbero avere tra loro. Occupandoci di filtrare segnali audio, invece, è necessario comprendere il concetto di fase.

Se io prendo una forma d’onda e la sposto rispetto a un riferimento temporale, avrò imposto a quella forma d’onda uno spostamento in fase. Prendendo ad esempio la forma d’onda più semplice, quella sinusoidale: se la sposto di un quarto di lunghezza d’onda rispetto a un riferimento qualsiasi, quello sarà il time shift, o phase shift. Espresso in gradi, una quarto di lunghezza d’onda sono 90°. Un semiciclo, cioè metà lunghezza d’onda, sono 180° eccetera. La ascolterò o la registrerò o la vedrò prima o dopo il riferimento preso. Niente altro.

Se invece prendo due sinusoidi e ne uso una come riferimento per l’altra, ecco che invece di avere a che fare con un punto di riferimento temporale di un segnale, avrò due segnali da mettere in relazione.
Qualora li volessi sommare e fossero due segnali identici, e se entrambi fossero perfettamente allineati temporalmente, non farei altro che sommare punto per punto ottenendo un segnale identico ma di ampiezza doppia.
Se li disallineo temporalmente l’uno con l’altro, cioè li sfaso, avrò fenomeni di comb filtering, filtro a pettine, di cui già ci occupammo. Sulle interferenze costruttive/distruttive sappiamo tutto e non ci torno.

È utile notare che è proprio grazie a due segnali shiftati che si fanno i time based effect come i flanger, i phasing eccetera. Le applicazioni e l’impiego dei comb filter è piuttosto esteso sia nel signal processing che nella sintesi sonora e in ogni campo al di fuori dell’acustica e dell’audio. Un filtro tipico nel signal processing è il filtro passa‑tutto, cioè che lascia passare tutte le frequenze senza attenuazioni di ampiezza bensì cambia la relazione di fase tra varie frequenze, modificandone il tempo, cioè il delay, di propagazione. Si usano, ad esempio, per compensare altre variazioni di fase esistenti in un sistema. Si identificherà una frequenza ben determinata ad avere un ritardo, un time shift, ad esempio di 90 gradi. È così che convenzionalmente si progetta un all‑pass, per la frequenza che passa per lo zero con un delay di 90 gradi.
Per vedere in moto la rappresentazione della relazione fra fase e delay temporale di un onda e un applet java sulla differenza di fase fra due onde, segnalo due link nel box in fondo. Speriamo che resistano per un po’ al loro posto, non sono stato molto fortunato con le ultime segnalazioni: le università spostano spesso le loro pagine e questi esempi non sono facili da trovare.

Adesso occupiamoci dei filtri che attenuano le frequenze, i passa‑alto e i passa‑basso. Una combinazione fra passa‑alto e passa‑basso stabilisce un filtro passa‑banda, è intuitivo. Un notch filter non è altro che un filtro molto stretto a pendenza elevata, particolarmente instabile e soggetto a fenomeni di ringing (quel suono di rrriiinng che segnala l’inizio della risonanza, tipico appunto del comb filtering dovuto al feedback).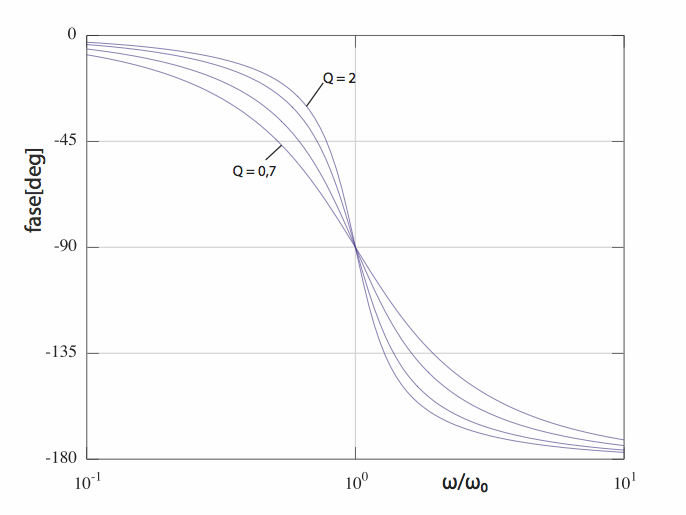

Ordine
I filtri del primo ordine si chiamano così perché richiedono un solo componente e hanno una pendenza di 6 dB per ottava.
I filtri del secondo ordine richiedono due componenti, condensatore e induttanza, ed hanno una pendenza di attenuazione di 12 dB per ottava. Tre componenti per il 18, e quattro per il 24 dB/ottava, cioè due condensatori e due induttanze.
Nella figura 1 riportiamo una serie di circuiti passa‑alto e passa‑basso in filtri passivi.

Caratteristiche del filtro
Avrete sentito parlare di filtri di Butterworth, di Bessel, di Linkwitz-Riley eccetera.
Un passa alto a 6 dB per ottava di tipo Bessel ha un comportamento in fase differente dal 6 dB per ottava con caratteristica Butterworth.
Oltre alla attenuazione espressa in dB/ottava e alla caratteristica dell’andamento di fase, cosa altro caratterizza un filtro?
Il suo “Q”, detto anche fattore di merito. Dal punto di vista dell’ampiezza, il Q si manifesta determinando l’andamento del “ginocchio” del filtro, cioè la zona di transizione tra la risposta piatta e l’inizio della pendenza. Un filtro con un Q pari a 2 avrà un picco, una gobba arrotondata, di +6 dB alla frequenza di taglio. Si dice che è un filtro sotto-smorzato, rispetto a un valore convenzionale che si prende a 1 o talvolta a 0,7.
Un Q più alto di 2 determinerà un picco sempre più alto e stretto. I grafici riportati in figura 2 mostrano le risposte in ampiezza e fase per diversi valori di Q.
Filtri attivi passa‑alti con Q=2 vengono ad esempio impiegati per allineamenti reflex del sesto ordine che permettono, a parità di volume di cassa e di spostamento del cono, di scendere maggiormente rispetto agli allineamenti B4. In pratica si utilizza una combinazione di cassa sovra-smorzata e filtro passa‑alti sotto-smorzato.
Per oggi mi fermerei qui.
La prossima volta vedremo come i filtri si combinano tra loro ma prima ancora, ricorrendo agli splendidi articoli di Linkwitz su Wireless World che mi fulminarono da ragazzo, vedremo l’influenza dell’ordine di filtro sul lobo di dispersione degli altoparlanti e cosa succede spostando in un due vie il piano virtuale di emissione relativo tra i due componenti, il woofer ed il tweeter.
Alla fine di queste letture, vi passerà la voglia di modificare le caratteristiche di taglio dei vostri impianti pistolando sui crossover elettronici. Oppure ve la farà venire.
Dipende.