Analogico Digitale: andata e ritorno - 5

di Mario Di Cola e Marta Furlan

Un bentornato ai nostri lettori! Facciamo un altro sforzo di concentrazione per completare insieme questo cammino sulla linea di confine tra il mondo analogico e quello digitale.

Andiamo dunque al sodo e dedichiamo la nostra attenzione all'analisi delle differenti tipologie di convertitori analogico-digitali esistenti, soffermandoci in particolar modo sui convertitori cosiddetti sigma-delta, che sono quelli di più largo impiego nel campo dell'audio.

Un passo in avanti...

È giunto il momento di andare a spiegare un po’ più nello specifico come funzionano i vari dispositivi. Dovremmo dunque parlare dei convertitori ADC ma, anche se vi suonerà strano, dobbiamo prima fare un salto in avanti ed andare a “spiare” i dispositivi che realizzano il percorso inverso, ovvero i convertitori digitali – analogici (DAC). Questo passo in avanti ci servirà perché, come scopriremo, molti ADC ospitano a bordo un DAC. Cosa se ne fanno? Nasce dunque prima il DAC o l’ADC? (… o se volete, prima l’uovo o la gallina?) In generale un DAC è tipicamente un dispositivo integrato dotato di un insieme di n ingressi digitali cui viene trasmesso il valore binario da convertire, e di un’uscita dalla quale è possibile prelevare, dopo un certo lasso di tempo prefissato, il risultato analogico della conversione. Il modo più accurato per effettuare una conversione AD è quella di avere incorporato nell’ADC un DAC al cui ingresso sono forzati una serie di codici binari che, convertiti dal DAC nei corrispondenti valori analogici, sono poi utilizzati per un confronto con il segnale analogico in ingresso all’ADC stesso (sembra complicato ma non lo è, fidatevi).

La tensione in uscita al DAC ha una dinamica compresa tra un valore minimo di riferimento (solitamente la massa, gli 0 Volt per capirci) e il valore massimo di fondo scala (Full Scale Range, FSR) che di solito è una tensione di poco inferiore alla tensione di alimentazione del dispositivo stesso. All’interno di quest’intervallo, la tensione d’uscita può assumere uno dei 2n valori possibili, corrispondenti alle 2n combinazioni degli n bit in ingresso al convertitore DAC.

Un parametro importante che descrive le prestazioni di un DAC commerciale è il cosiddetto range dinamico (DR), che rappresenta la differenza espressa in dB tra il minimo ed il massimo valore analogico rappresentabile. Il DR dipende dal numero di livelli disponibili (più sono, più l’intervallo tra due livelli sarà una frazione minima del FSR) ed in ultima analisi è legato al numero di bit del DAC. Tale legame può essere espresso in linea teorica con un’ottima approssimazione dalla seguente relazione pratica: DR in dB 20 log10(2n)= 6,02n dove n ricordiamo è il numero di bit. Questo valore della gamma dinamica è quello che il convertitore DAC dovrebbe raggiungere teoricamente, grazie al suo numero di bit. Stando a questi calcoli, un DAC da 16bit dovrebbe darvi in uscita ben 6,02 * 16 = 96,32dB di gamma dinamica. Nella realtà, questo valore non può essere raggiunto in quanto il rumore di fondo dovuto al circuito in cui è inserito, insieme al rumore che esso stesso genera fa si che la gamma dinamica realmente a disposizione sia un po’ inferiore a quella teorica.

In questo senso, è pratica diffusa soprattutto nel mondo Hi-Fi definire una risoluzione “effettiva” in bit, usando all’inverso la formula appena vista e partendo da un dato di gamma dinamica misurato. E’ chiaro che il risultato che se ne ottiene non è necessariamente un numero intero: può anche essere un numero decimale. Va da se che se dovesse venire fuori che il vostro DAC da 16 bit ha una risoluzione effettiva di 14,3 bit ciò non significa (ovviamente) che il convertitore abbia davvero 14,3 di bit. Questo non sarebbe possibile in quanto il numero di bit può essere solo intero. Il vero significato è che se il vostro DAC pur avendo un’architettura a 16 bit, a causa di vari rumori non eliminabili, fornisce in uscita una gamma dinamica di circa 86dB allora il DAC si comporta come se di bit ne avesse solo 14 e poco più. Poiché una certa quantità di rumore rimane sempre e non può essere eliminata del tutto è impossibile sfruttare le architetture dei DAC (e vedremo anche degli ADC) fino all’ultimo bit.

Di solito l’ultimo e meno significativo bit (detto anche Least Significant Bit, LSB) di quelli disponibili, è privo di vero significato per la maggior parte del tempo durante la riproduzione di un segnale. Esso di solito commuta casualmente tra 1 e 0 stando proprio a rappresentare un rumore casuale. E c’è da dire che quando alla risoluzione effettiva manca un solo bit per raggiungere quella teorica le cose vanno già alla grandissima. Di solito la situazione è molto peggiore. Ci sono alcuni lettori CD di scarsa qualità che dei 16 bit teorici ne hanno effettivi poco più di 12! E che dire delle schede audio da ben 24 bit che hanno ultimamente invaso il mercato a costi talvolta irrisori? Se ne trovate una con 18 o 19 bit di risoluzione effettiva potete gia ritenervi contenti e soddisfatti!!

Architetture ADC

Torniamo sul seminato ed andiamo a vedere un po’ come possono essere fatti gli ADC.

Ricordiamo che i convertitori ADC sono quei dispositivi che si occupano di tradurre il segnale analogico fornito al loro ingresso nelle corrispondenti parole binarie, ovvero in sequenze di valori di tensione "bassi" o "alti", i quali saranno poi letti dai dispositivi digitali di elaborazione/memorizzazione come sequenze di "0" e "1".

L’operazione di conversione effettuata da un ADC è suddivisibile a livello logico - ma anche a livello architetturale -, in due passi fondamentali: la quantizzazione vera e propria del dato analogico e poi la digitalizzazione del dato. È vero che queste due operazioni finora le abbiamo sempre riunite sotto l’unica etichetta di “quantizzazione” ma tant’è, ora che ci addentriamo nello specifico è meglio precisare. Quello che avviene è che in una prima fase il dato analogico in ingresso è quantizzato, ovvero gli viene assegnato un ben preciso intervallo di valori (un “gradino” della scalinata della figura 1.) ; in una seconda fase il dato viene digitalizzato, cioè viene assegnata una precisa codifica binaria associata al gradino individuato.

Come abbiamo già avuto modo di spiegare, è prassi comune impiegare a monte di un circuito ADC il cosiddetto circuito S&H (Sample&Hold), il quale ha la funzione di mantenere "stabile" il dato analogico in ingresso all'ADC, almeno per tutto il tempo impiegato dall'ADC a convertire il campione. Infatti, se il segnale analogico non è stabile ma varia "significativamente" (di una quantità superiore a ±1/2 LSB) proprio mentre l'ADC è ancora impegnato a convertirlo, la conversione può risultare errata, in quanto come vedremo i bit digitali in uscita all'ADC non sono asseriti né istantaneamente né contemporaneamente.

Prima di passare a fare una panoramica delle diverse architetture di ADC, premettiamo che ciascun dispositivo ADC necessita di due valori di tensione di riferimento tra le quali operare: Vref (valore massimo corrispondente ad un codice di uscita contenente tutti "1") e Vlow (valore minimo, solitamente massa, corrispondente ad un codice di uscita contenente tutti "0"). Ricordiamo infine che la caratteristica della conversione analogico-digitale è che ogni codice binario d’uscita corrisponde ad un intervallo analogico di valori in ingresso, il quale può variare con continuità. La larghezza di questi intervalli per un ADC a n bit è Vref/2n (la quantità detta "LSB"). La conversione analogico digitale è pertanto sempre e comunque affetta da un errore non eliminabile, di ampiezza massima ½ LSB, dovuto alla quantizzazione del segnale analogico tramite la scalinata caratteristica dell'ADC. La figura 1 mostra la caratteristica ideale di un ADC (ideale perché sono supposti nulli gli errori di offset e di gain in realtà presenti) e il corrispondente andamento dell’errore di quantizzazione ε. Notiamo che l’errore è massimo per quei campioni analogici che “cascano” proprio in mezzo all’intervallo di quantizzazione, in quanto il convertitore deve “decidere” se assegnare al campione uno dei due codici digitali che corrispondono ai due estremi dell’intervallo.

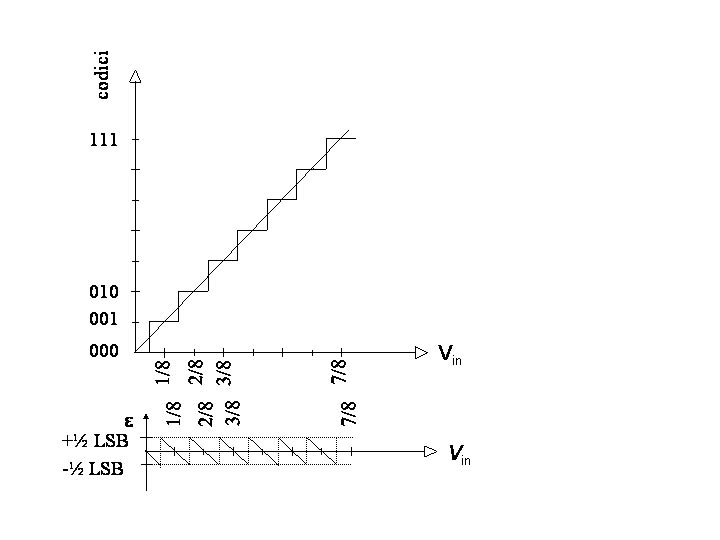
Figura 1. Caratteristica statica ideale di un convertitore ADC a 3 bit e corrispondente andamento dell'errore di quantizzazione ε

Il primo convertitore che esaminiamo è l'ADC flash: esso su basa su un’idea molto semplice. L’idea è quella di usare un semplice partitore resistivo allo scopo di creare i diversi livelli di quantizzazione. L’intervallo di riferimento (compreso tra la massa e Vref) è infatti ripartito in intervalli di uguale ampiezza misurabili ai capi delle resistenze. Insomma, abbiamo fatto tanta strada e siamo ancora al partitore resistivo cioè alla legge di Ohm! L’idea è dunque quella di applicare il valore analogico di tensione in ingresso ad una “batteria” di comparatori. Ciascun comparatore realizza il confronto tra la tensione di riferimento (quella che si sviluppa ai capi della specifica resistenza associata al comparatore, vedi Figura 2) e la tensione del segnale in ingresso Vin. L’uscita del particolare comparatore scatta al livello di tensione "alto" non appena l'ingresso supera il valore di tensione di riferimento ai capi della resistenza corrispondente. In questo modo è possibile stabilire l'intervallo di valori di tensione all'interno del quale "casca" il campione da convertire. L'encoder digitale alla fine trasforma tale codifica in una sequenza di n bit che identificano l'intervallo.

L’ADC flash prende il nome dalla rapidità con cui effettua la conversione, pari solo al tempo di comparazione sommato al tempo di codifica. Purtroppo lo svantaggio è dato da un vincolo architetturale che impone di utilizzare 2n comparatori per ottenere una codifica a n bit, in quanto ognuno di essi si pone a definire un singolo livello, il che non è poco: per 8 bit occorrono 255 comparatori in modo da segnalare tutti i 256 livelli. Inoltre all'aumentare del numero di bit, si fanno sempre più consistenti le non linearità dovute alle tolleranze del partitore ed alla sua alterazione causata dalle correnti di leakage e bias e capacità parassite agli ingressi dei comparatori. I convertitori Flash, grazie alla loro elevata velocità di conversione, sono utilizzati laddove sono necessarie altissime frequenze di campionamento, dell’ordine dei MegaHertz o GigaHertz. A causa però della loro complessità architetturale sono praticamente realizzabili solo quando il numero di bit necessari è piuttosto basso.

Essi sono utilizzati principalmente in apparecchiature di misura e per dispositivi che operano nel campo dell’alta frequenza.

Figura 2. Schema di un convertitore flash

Nell’architettura ADC Flash non si fa uso del DAC, cosa che invece vediamo nelle successive.

Il convertitore a gradinata vale la pena di essere illustrato perché funziona in base ad un meccanismo alquanto ingegnoso. Non è di impiego pratico nel campo dell’audio ma merita di essere visto poiché istruttivo.

L'idea alla base di questa configurazione è quella di modificare con successivi aggiustamenti il codice binario in ingresso al DAC, fino a che la tensione in uscita al DAC non raggiunge il valore del segnale da convertire (Vin): il codice che realizza tale conversione sarà l'uscita finale dell'ADC.

Per fare ciò il DAC è alimentato da un contatore binario (comandato da un clock) che forza una "gradinata" (una sequenza di “scalini” di tensione) in ingresso al DAC stesso. Il processo di conteggio terminerà quando la tensione in uscita al DAC supera la tensione di ingresso al convertitore: a quel punto la commutazione del comparatore (realizzato mediante OpAmp) e di conseguenza la commutazione del contenuto del registro blocca il clock del contatore assicurando che il valore contenuto nel contatore è il codice digitale desiderato.

E' ovvio che la precisione della conversione A/D dipende da quella del DAC. E il tempo di conversione può arrivare anche a 2n periodi di clock, quando l'ingresso è massimo e il contatore deve arrivare alla parola binaria costituita da tutti 1. In formule, il tempo di conversione massimo di un ADC a gradinata è pari a Tconvmax = 2n/ fclock

La presenza di un tempo conversione massimo fa si che la frequenza del segnale di ingresso all’ADC, in assenza di un apposito S&H sia limitata ad un certo valore. Se infatti non c’è S&H, lasciamo all’ADC tutto il compito di prendere il segnale analogico e di convertirlo. Il segnale analogico però non deve variare troppo velocemente, perché in tal modo è possibile che l'ADC non faccia a tempo a convertire e si trovi all'ingresso un valore del segnale sostanzialmente diverso da quello che si sarebbe dovuto osservare. Comunque, il fatto che tali convertitori non siano adatti ai segnali audio lo si capisce facilmente dalla seguente considerazione: avendo il vincolo che i campioni siano spaziati di un tempo pari almeno a Tconvmax, per il teorema del campionamento, la frequenza massima del segnale in ingresso all’ADC deve essere pari a 1/ 2 Tconvmax. Questo significa che con un ADC a 10 bit con fclock di 10 MHz, avremo Tconvmax pari a 0.1msec e frequenza massima del segnale di solo 5kHz!

Si potrebbe pensare di aumentare la frequenza di clock, ma questa a sua volta non può crescere a dismisura poiché è limitata alla velocità del DAC e del comparatore: tra due istanti di clock devono accadere un sacco di cose:incremento del clock, assestamento dell’uscita del DAC e eventualmente lo “scatto” del comparatore.

Figura 4. Andamento del segnale analogico in ingresso all'ADC (supposto continuo) e segnale digitale in uscita per un ADC a gradinata. In alto il segnale in rosso identifica la gradinata che viene forzata all’interno del DAC. La caratteristica da notare è che il tempo di conversione tra un dato digitale e l'altro diminuisce al diminuire del valore di tensione in ingresso.

L'ADC a inseguimento (tracking) ospita un DAC all'interno. Il suo funzionamento si basa anche in questo caso su di un’idea furba. La struttura è simile a quella di un convertitore a scalinata ma il suo contatore binario non viene resettato e incrementato ad ogni nuova conversione come nel caso precedente. Esso viene fatto incrementare o decrementare a seconda se la tensione in ingresso Vin sia maggiore o minore di quella fornita dal DAC. In questo modo all'inizio del funzionamento, dopo una prima fase di gradinata, e se il segnale in ingresso varia "abbastanza" lentamente, il DAC lo insegue in un numero ridotto di impulsi di clock, e al limite rimane agganciato ad ogni impulso di clock.

Per fare ciò serve un contatore up-down pilotato da una semplice logica che sfrutta l'uscita del comparatore.

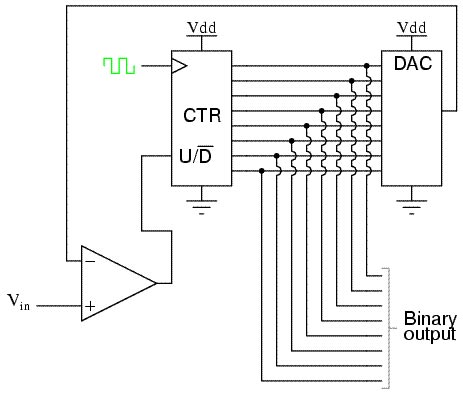
Figura 5. Schema di un ADC tracking

Questo ADC è molto più veloce del precedente, in quanto dopo la fase iniziale è in grado di fornire un codice binario in uscita ad ogni colpo di clock. Il problema è che l'uscita di questo ADC non è stabile, neppure con segnali analogici in ingresso stabili. Il problema è aggirabile per mezzo di un registro a valle dell'ADC che registra ad esempio un codice binario ogni due.

Sia per questo che per il precedente sistema, il tempo di conversione del dato analogico dipende dal valore stesso del segnale. Questi ADC pertanto non possono garantire una sequenza di dati regolare in uscita. Per ovviare a quest’inconveniente è utile il circuito S&H a monte dell’ADC: si fa derivare il segnale SoC (start of conversion) dal comando del S&H che dà il via al campionamento sfasandoli opportunamente secondo i tempi di settling del S&H, e si prelevano solo i dati in uscita dall’ADC alla frequenza del segnale SoC (presupponendo che comunque il tempo di conversione dell’ADC , se abbiamo fatto le cose bene, sia ovviamente inferiore al periodo di campionamento: in questo modo siamo sicuri che il campione successivo arrivi da convertire al ADC solo dopo che è terminata la conversione del precedente).

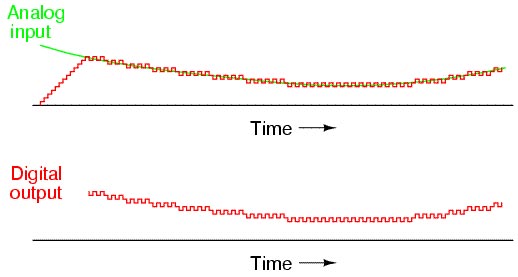
Figura 6. Ingresso e uscita di un ADC tracking con andamento del segnale digitale forzato all’ingresso del DAC (in alto in rosso)

L' ADC a singola rampa si basa su un principio simile a quello a gradinata, con la differenza che sfrutta una rampa analogica e non una gradinata digitale per effettuare la comparazione e non necessita di un DAC, ma di un generatore di corrente costante e di un MOS. Anche in questo caso il comparatore di stop serve a decretare il completamento della conversione effettuando il confronto tra la tensione in ingresso e il valore della rampa.

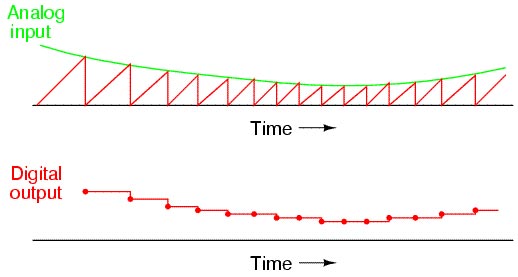
Figura 8. Ingresso e uscita di un ADC a singola rampa

I convertitori visti fino ad ora non sono granché utilizzati nell’audio. Essi sono dedicati al rilevamento di segnali provenienti da sensori di vario tipo o da specifici strumenti di misura dedicati ad altri campi. La breve panoramica serve ai curiosi e secondo noi aiuta a capire meglio cosa serve ad un convertitore audio.

L'ultimo ADC della veloce rassegna è l'ADC SAR (o ad approssimazioni successive). Questo convertitore compie una ricerca binaria del codice corrispondente al valore analogico Vin, riuscendo a trovare il codice in un tempo pari al numero di cicli di clock per il numero di bit in uscita, grazie alla cosiddetta “ricerca binaria”. In questo senso l'ADC SAR si differenzia dai precedenti in quanto avremo un segnale digitale in uscita costituito da campioni equispaziati nel tempo.

L'ADC SAR è pilotato da una apposita logica in grado di asserire di volta in volta 1 bit in ingresso al suo DAC interno, cominciando dal bit più significativo e di confrontare il corrispondente valore analogico (corrispondente a metà della scala di valori possibili, ovvero a Vref/2) generato dal DAC, con la tensione in ingresso: se Vin è superiore all'uscita del DAC, il bit è mantenuto a 1, altrimenti portato a 0. Ad ogni colpo di clock il SAR asserisce un bit alla volta, sino al meno significativo. Ogni conversione richiede solo n+1 impulsi di clock per essere portata a termine, permettendo al convertitore di trattare con segnali di frequenza maggiore di un fattore 100 rispetto all'ADC a singola rampa nel caso di 10 bit. Tale miglioramento della velocità di conversione rispetto agli altri ADC è tanto più consistente quanto più aumenta il numero di bit, poiché l'ADC SAR lega il tempo di conversione al numero di bit con una relazione lineare, anziché esponenziale come negli altri casi.

L'unico vincolo è che il segnale in ingresso resti costante per tutto il tempo della conversione: per far ciò è necessario in questo caso anteporre al all'ADC un semplice S&H con l'introduzione di opportuni segnali di sincronizzazione tra i due stadi di campionamento e quantizzazione.

Figura 10. Ingresso e uscita di un ADC SAR: i codici binari in uscita sono forniti ad intervalli temporali equispaziati

Bene, abbiamo visto questa veloce panoramica su come gli ADC sono implementati. Nessuna pretesa di spiegarli (ovviamente) con queste poche righe a chi li progetta. C’è da dire che i convertitori SAR sono stati gli unici, tra quelli visti sinora, ad essere utilizzati con qualche successo nell’audio. Tale utilizzo in alcuni casi (ad es. nel caso delle schede di misura per elettroacustica) è continuato almeno fino all’inizio degli anni novanta. Sappiamo tuttavia che da lungo tempo la tecnologia di conversione imperante nel mondo dell’audio è quella dei convertitori cosiddetti Sigma-Delta. Ed è proprio da li che inizieremo la prossima volta entrando nel vivo della tecnologia contemporanea.

A presto.

CLICCA QUI PER ACCEDERE ALLA SESTA PARTE