I filtri digitali - terza parte
I filtri IIR (ricorsivi, con risposta all'impulso infinita).
Nei due numeri scorsi sono stati presentati i filtri FIR. Proseguiamo qui descrivendo i filtri IIR, chiamati anche filtri ricorsivi.
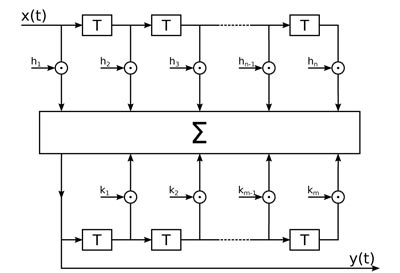
Figura 1: Schema a blocchi di un filtro ricorsivo.
Ho già scritto in precedenza che i filtri digitali, FIR o IIR che siano, sono fatti di calcoli. Il segnale viene campionato, i campioni vengono trasformati in numeri e con questi numeri, che rappresentano il segnale di ingresso al filtro, si fanno i calcoli. Il risultato del calcolo, aggiornato ad ogni campione, rappresenta l’uscita del filtro: la serie temporale dei numeri generata dal calcolo viene trasformata in un segnale (elettrico, in genere) e riprodotta.
Come per i filtri FIR descritti nei precedenti articoli, il calcolo può utilizzare un certo numero di campioni tra quelli arrivati in ingresso nel passato, di solito nel passato recente. Questo è tutto quello che fanno i filtri FIR: una serie di moltiplicazioni e somme che utilizzano gli ultimi n campioni in ingresso.

Un filtro reale, ovviamente, non può utilizzare i campioni futuri, dato che ancora non esistono. Può però utilizzare i valori già calcolati in precedenza, i risultati dei calcoli che hanno finora formato l’uscita del filtro. È, in pratica, una retroazione: il segnale d’uscita viene riportato in ingresso e contribuisce a formare i dati su cui viene eseguito il calcolo per ricavare i nuovi valori dell’uscita.

In altri termini, ciascun singolo campione del segnale in uscita è calcolato moltiplicando i numeri corrispondenti agli ultimi campioni in ingresso per una serie di coefficienti h, gli ultimi valori già calcolati del segnale in uscita per una serie di coefficienti k e sommando poi tra loro i risultati.
La risposta all’impulso di un filtro ricorsivo è, in genere, un’oscillazione smorzata. Di fatto, per i filtri IIR, la risposta all’impulso non è necessariamente finita. Anzi: se non si fa particolare attenzione alla scelta dei coefficienti, un filtro IIR può facilmente risultare instabile, cioè la risposta all’impulso può non essere sufficientemente smorzata e divergere crescendo nel tempo anche in corrispondenza ad un ingresso limitato o finito.
In genere, il numero di coefficienti utilizzabili per il calcolo di un filtraggio ricorsivo è limitato ad una diecina o poco più, altrimenti diventa davvero difficile mantenere il filtro stabile, cioè mantenere limitato il segnale d’uscita.
I coefficienti dei filtri IIR sono calcolati tramite un metodo simile a quello utilizzato per il progetto dei filtri analogici, passando attraverso un procedimento matematico che fa uso di uno strumento detto trasformata z, strumento del tutto analogo a quella che nel dominio analogico è la trasformata di Laplace, tramite la quale si formalizza il concetto di funzione di trasferimento. In pratica, data la risposta in frequenza desiderata, si determina la funzione di trasferimento in termini di trasformata e da lì, anti-trasformando, si determinano i coefficienti effettivi. Si tratta di un procedimento relativamente complesso, ma è cosa per addetti ai lavori e non è il caso di addentrarci qui nei particolari.
Proprio come con i filtri analogici, ciascun filtro si può pensare composto di una cascata di più stadi di filtraggio relativamente semplici, del primo o del secondo ordine. Nel caso digitale, poi, i diversi stadi vengono combinati in un’unica serie di coefficienti.
Un semplice filtraggio passa-basso dei primo ordine, ad esempio, corrispondente all’azione del circuito di figura 2, si può ottenere con un semplice filtro IIR a due coefficienti, uno per il segnale di ingresso ed uno per l’uscita precedente.

Figura 2: Un filtro passa-bassi analogico del primo ordine
![]()
Scegliendo opportunamente i coefficienti, così come i componenti elettronici, il filtro passa basso analogico di figura 2 ed il filtro passa-bassi digitale IIR possono presentare la stessa risposta. Utilizzando, ad esempio

per il filtro digitale e

per il filtro analogico, si ottiene in entrambi i casi un filtro passa-bassi con frequenza di taglio a ‑3 dB pari a 320 Hz (su un segnale campionato a 48 kHz, nel caso del filtro digitale) e guadagno in continua unitario.
La risposta temporale ad un gradino di tensione, valida sia per il filtro analogico che per il filtro digitale, è riportata in figura 3.

Figura 3: risposta al gradino di un filtro passa-bassi, analogico o digitale IIR.
Il vantaggio dei filtri IIR rispetto ai filtri FIR risiede nel fatto che comunque, con una diecina di coefficienti, la performance in frequenza di un filtro IIR può essere decisamente migliore rispetto ad un filtro FIR di pari lunghezza, soprattutto (e anche di gran lunga) quando le frequenze di taglio sono molto basse o molto alte (rispetto alla frequenza di campionamento). In questo caso con la parola performance intendo la ripidità della banda di transizione, ovvero la capacità di separare frequenze relativamente vicine.
Ci sono anche degli svantaggi, ovviamente. Il principale svantaggio dei filtri IIR è che, mentre è possibile realizzare filtri FIR a fase lineare, i filtri IIR presentano in genere una distorsione di fase, in maniera del tutto simile, anche in questo caso, ai convenzionali filtri analogici.
Se dal punto di vista analogico, hardware, un limite è rappresentato dalle non-idealità dei componenti utilizzati, nel dominio digitale il limite è dato di fatto dalla precisione finita e dunque dagli inevitabili errori di arrotondamento nei calcoli.
In ogni caso, con pochi coefficienti, quindi con pochi calcoli e pochi errori, si riescono ad ottenere filtri IIR con ottime performance, se paragonati ai corrispondenti analogici.




