I Filtri digitali - seconda parte

di Michele Viola

 Nel numero scorso sono stati presentati gli schemi concettuali e implementativi dei filtri FIR e IIR, anche detti, rispettivamente, filtri trasversali e filtri ricorsivi. È stato poi analizzato un filtro FIR passa-bassi più semplice possibile: la media mobile, suscettibile anche di una implementazione ricorsiva particolarmente efficace. Proseguiamo descrivendo più nel dettaglio i filtri FIR, ovvero i filtri con risposta all’impulso finita.

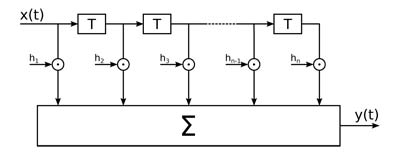
Figura 1: Schema a blocchi di un filtro trasversale.

I filtri FIR

Il filtro a media mobile presentato nel numero scorso corrisponde al filtro FIR dello schema di figura 1, nel quale gli n coefficienti sono tutti pari ad 1/n. Ritornando sull’esempio del numero scorso, riguardante il calcolo della media mobile a cinque punti, si può scrivere:

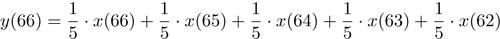
Nel caso generale, invece, i coefficienti di un filtro FIR possono essere anche tutti differenti tra loro:

La successione dei coefficienti hi prende il nome di nucleo (o, più comunemente, in lingua inglese, kernel) del filtro. In questo modo, il calcolo non è più una media mobile e non è più possibile, in generale, un’implementazione così parca di risorse come quella ricorsiva per la media mobile presentata nel numero scorso. Non siamo più legati, peraltro, alla realizzazione di un filtro passa-bassi; è anzi così possibile riprodurre, seppure con una certa approssimazione, qualunque risposta in frequenza desiderata. L’approssimazione sarà tanto migliore quanto più il filtro è lungo, cioè all’aumentare del numero di coefficienti (e, quindi, del numero di campioni utilizzati per il calcolo) la risposta reale approssimerà con maggiore precisione la risposta desiderata (figura 2). La qualità della risposta sarà quindi legata alla complessità di calcolo.

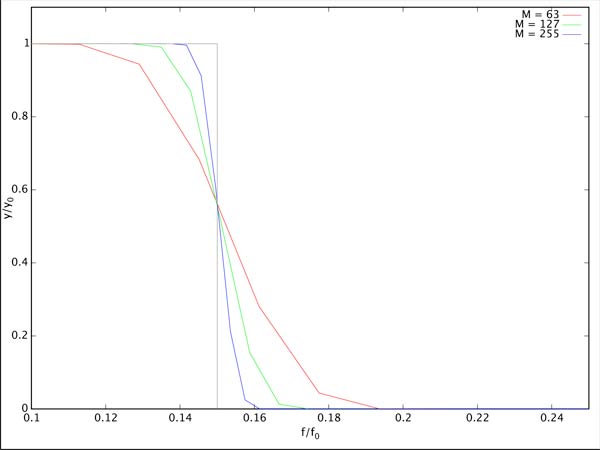
Figura 2: Risposta in frequenza ideale (in grigio) e reale di un filtro FIR per diverse lunghezze del kernel.

Non è il caso di addentrarci, in questa sede, nei dettagli dei calcoli necessari per produrre un filtro FIR con una data risposta in frequenza.

Una considerazione che vale invece la pena di fare qui è che il principale punto di forza di un filtro così fatto è la possibilità di ottenere una risposta in fase ideale. In pratica, una volta superato il transitorio dei primi n campioni dall’istante di applicazione, un filtro FIR lungo n passi introduce un ritardo costante pari a n/2, indipendente dalla frequenza (figura 3).

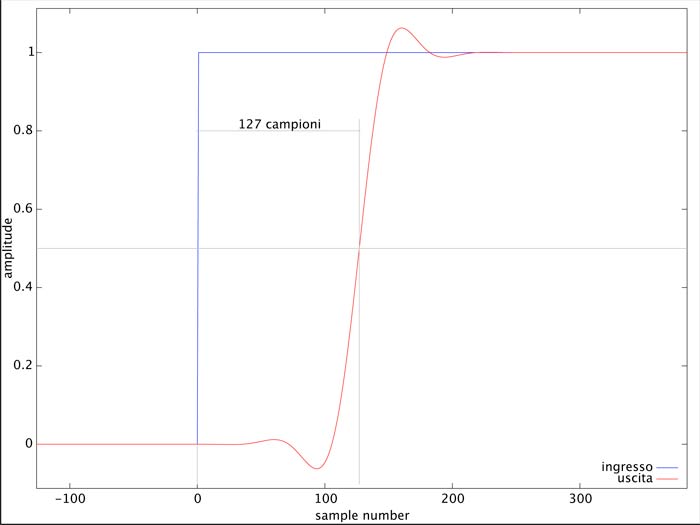
Figura 3: Ingresso e risposta al gradino unitario di un filtro FIR passa-bassi a 255 passi.

Essendo il ritardo costante e indipendente dalla frequenza, un filtro siffatto è privo di distorsione di fase. Da notare l’assenza di avverbi come “quasi” o “praticamente”: la risposta in fase non è “quasi ideale”, è proprio ideale nel senso stretto; semplicemente, in questo caso, il problema della distorsione di fase non si pone.

D’altro canto, per avere un’approssimazione in ampiezza sufficiente con risposte in frequenza arbitrarie possono essere necessari molti termini, dunque il segnale diventa disponibile dopo un transitorio iniziale che può essere rilevante, il ritardo introdotto può anch’esso non essere trascurabile e, inoltre, il calcolo del filtro può richiedere notevoli risorse di calcolo.

Perché si chiama “FIR”?

Un filtro FIR è quindi composto dalla somma di un numero finito, anche se eventualmente elevato, di campioni successivi del segnale, ciascuno dei quali eventualmente moltiplicato per un opportuno coefficiente. Immettendo in ingresso al filtro un singolo impulso, cioè un singolo campione diverso da zero circondato da campioni nulli, l’effetto dell’impulso si ritroverà in uscita al più per n intervalli, perché l’uscita è composta dall’elaborazione di n campioni.

Dato che stiamo parlando di calcoli, una certa formalizzazione può aiutare a esprimere il concetto in maniera più chiara. Immettendo in ingresso a un filtro FIR a cinque passi un impulso formato da un singolo campione non nullo all’istante di campionamento 1:

In altri termini:

L’uscita del filtro, dal sesto campione in poi, non potrà avere memoria dell’impulso trascorso, perché nel calcolo non c’è più x(1):

...

Per questo si chiama FIR, cioè Finite Impulse Response: poiché il numero n di campioni elaborati è finito, allora la risposta all’impulso termina anch’essa, al più dopo n campioni. In altri termini, e questa è senz’altro un’ulteriore caratteristica particolarmente interessante, non oscilla, cioè se l’ingresso termina anche l’uscita terminerà in un tempo finito.

La distorsione di fase

Forse è il caso di approfondire un poco il concetto di distorsione di fase.

Nell’ambito del trattamento dei segnali, la fase corrisponde, in pratica, alla posizione nel tempo, cioè all’istante. La distanza temporale tra due eventi si può quindi in qualche modo associare ad uno sfasamento, cioè ad una differenza di fase.

I dispositivi di elaborazione del segnale agiscono, in generale, sull’ampiezza e sulla fase. In altri termini, un segnale in ingresso sarà, in generale, modificato in ampiezza e ritardato nel tempo.

La distorsione corrisponde all’aggiunta di componenti indesiderate; si può dire che un dispositivo dedicato all’elaborazione del segnale distorce quando la sua uscita non corrisponde esattamente al risultato desiderato dell’elaborazione stessa.

Se l’elaborazione non modifica la forma del segnale ma solamente l’ampiezza in maniera uniforme, allora sicuramente non c’è distorsione. Una sinusoide può essere amplificata o attenuata uniformemente e anche, al limite, traslata nel tempo: finché rimane una sinusoide pura, si può considerare non distorta.

Un segnale reale si può pensare, in genere, composto di più sinusoidi, ciascuna con la propria ampiezza e con la propria fase. L’insieme delle sinusoidi che formano il segnale si chiama spettro del segnale stesso. La forma del segnale complessivo è associata alla sua composizione spettrale, cioè dipende dalle ampiezze e dagli sfasamenti (ritardi) reciproci tra le sinusoidi che compongono lo spettro.

Se un dispositivo ha l’unico effetto di ritardare tutte le componenti del segnale della stessa quantità temporale, allora la forma dell’onda in uscita corrisponde a quella dell’onda in ingresso. Se il ritardo applicato alle singole sinusoidi non è costante, allora la forma d’onda in uscita è diversa dalla forma d’onda in ingresso, quindi viene introdotta una distorsione. Nella figura 4 è rappresentato un segnale formato dalla somma di due sinusoidi, in alto, ed un altro segnale, in basso, formato dalla somma delle stesse due sinusoidi ma di cui solo la seconda è ritardata di un breve intervallo di tempo. Osservando attentamente le due forme d’onda, si può notare che i due segnali non hanno la stessa forma. Il ritardo di fase influisce quindi sulla forma d’onda, per cui è in grado di distorcere un segnale.

L’orecchio umano non è molto sensibile alla distorsione di fase, nel senso che i due segnali rappresentati in figura 4 risulterebbero, nella maggior parte dei casi, praticamente indistinguibili all’ascolto. Le fasi reciproche possono però risultare molto importanti nei casi in cui l’interferenza tra più segnali svolga un ruolo significativo come, ad esempio, nella composizione del fronte d’onda di un line-array, oppure nelle percezioni di spazialità di un programma stereofonico o surround.

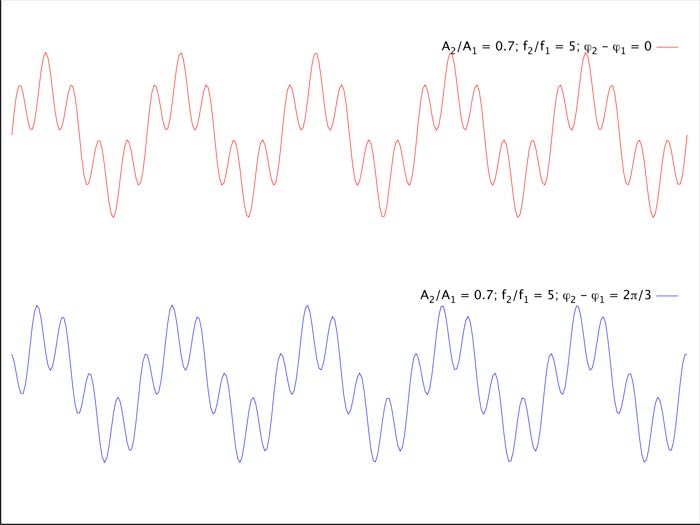
Figura 4: Le due forme d’onda sono composte delle stesse due sinusoidi, sfasate diversamente nel tempo.

L’assenza di distorsione di fase tipica dei filtri FIR rappresenta quindi un notevole vantaggio nell’elaborazione dei segnali implementata, ad esempio, in controller e processori per sistemi PA, o nei processori surround, per non parlare di utilizzi, peraltro ancora semi-esoterici, come gli ambienti di riproduzione Ambisonics o simili dove lo sfasamento reciproco dei segnali provenienti dai vari trasduttori deve necessariamente essere controllato con molta attenzione.