I Filtri digitali - prima parte

di Michele Viola

L’arguto Cantadori ha avuto modo, nei suoi scritti sulla presente rivista, di accennare più volte l’argomento “filtri” (anche nel senso, del tutto appropriato, di “setacci”). Nei numeri 88 e 89, in particolare, c’era qualcosa più di un cenno sui filtri digitali. Proviamo qui ad approfondire un poco alcuni dettagli teorici e implementativi.

I filtri digitali, a differenza di quelli analogici, agiscono direttamente su un segnale numerico e sono fatti di calcoli: somme, moltiplicazioni, ritardi.

Il funzionamento dei filtri digitali è basato sul concetto di comb filtering: sommando un segnale con una sua copia ritardata (figura 1), si ottiene un filtraggio, ovvero alcune frequenze risulteranno esaltate mentre altre frequenze risulteranno attenuate.

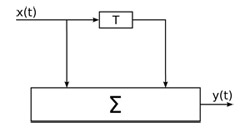
Figura 1: schema a blocchi di un comb filter.

In particolare, le frequenze per cui il ritardo corrisponde a un multiplo intero della lunghezza d’onda saranno raddoppiate in ampiezza, mentre le frequenze per cui il ritardo corrisponde a un multiplo dispari di mezza lunghezza d’onda risulteranno virtualmente annullate o comunque fortemente attenuate. La risposta in frequenza di un filtro siffatto, composto di un ritardo e di una somma, è riportata in figura 2.

Figura 2: risposta in frequenza di un comb filter.

È possibile, naturalmente, sommare più di due copie del segnale, ciascuna con un proprio ritardo. Le diverse copie del segnale possono anche essere singolarmente amplificate o attenuate prima della sommatoria. I componenti (digitali o analogici) che realizzano questa funzione si chiamano filtri trasversali o anche, forse più comunemente nel caso dei filtri digitali, filtri FIR. Lo schema a blocchi di un filtro trasversale è riportato in figura 3.

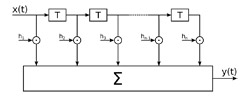
Figura 3: schema a blocchi di un filtro FIR.

Ci sono, sostanzialmente, due tipi di filtri digitali: i filtri FIR (Finite Impulse Response, tradotto: Risposta all’Impulso Finita), detti anche filtri trasversali, ed i filtri IIR (Infinite Impulse Response, cioè Risposta all’Impulso Infinita), detti anche filtri ricorsivi.

I segnali digitali si possono pensare composti di una successione equispaziata di impulsi. Sommare copie del segnale ritardate significa semplicemente sommare diversi campioni successivi nel tempo. I campioni possono essere ciascuno moltiplicato per un determinato coefficiente, prima della somma. Lo sfasamento temporale tra due campioni successivi nel tempo è pari al periodo di campionamento.

A differenza dei filtri FIR, i filtri ricorsivi (IIR) utilizzano per il calcolo del segnale d’uscita anche un certo numero di valori precedenti del segnale d’uscita stesso. In altri termini il segnale d’uscita, oltre a proseguire verso i blocchi di elaborazione successivi, è riportato, in diverse copie ritardate tra loro, in ingresso al filtro. Lo schema a blocchi di un filtro ricorsivo è riportato in figura 4.

Figura 4: schema a blocchi di un filtro IIR.

Da notare che il filtro trasversale di figura 3 si può pensare come un caso particolare del filtro di figura 4, corrispondente al caso in cui tutti i coefficienti moltiplicatori ki sono nulli. Se, invece, sono i coefficienti hi nel filtro ricorsivo di figura 4 ad essere tutti nulli (tranne il primo), cioè se l’uscita del filtro dipende solamente dai valori precedenti dell’uscita e dall’ingresso attuale ma non dai valori precedenti del segnale di ingresso, allora il filtro si chiama puramente ricorsivo ed il relativo schema a blocchi è riportato in figura 5.

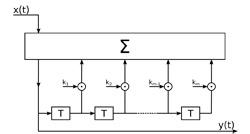
Figura 5: schema a blocchi di un filtro IIR puramente ricorsivo.

La media mobile

Un filtro FIR particolarmente semplice, nonché significativo, è quello in cui i coefficienti moltiplicativi sono tutti uguali: questo corrisponde, in pratica, a calcolare la media aritmetica degli ultimi n campioni. Questo tipo di calcolo si chiama media mobile. Mobile perché, pur coinvolgendo un numero fisso di termini, l’intervallo temporale su cui è eseguita la media avanza con il segnale. Per calcolare un campione di una media mobile a cinque punti, ad esempio, occorrono gli ultimi cinque campioni del segnale da elaborare:

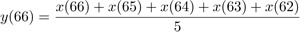
Per il campione successivo, serviranno ancora gli ultimi cinque campioni (quindi via il primo e dentro l’ultimo):

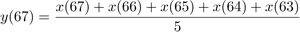
Dal punto di vista dell’elaborazione del segnale, la media ovviamente smorza le variazioni, ovvero si comporta come un filtro passa-basso.

Per molti aspetti, in verità, non è un gran filtro passa-basso. L’attenuazione in banda oscura non è un granché e, contemporaneamente, la pendenza è piuttosto blanda.

La risposta in frequenza (in dB) della media mobile, per diverse lunghezze della media, è riportata in figura 6. Da notare gli zeri della risposta in frequenza alle frequenze multiple intere dell’inverso del periodo della media: per la media ad m punti il primo zero è alla frequenza f0/m.

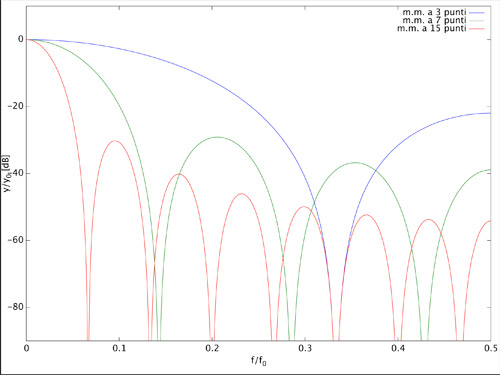
Figura 6: risposta in frequenza della media mobile, in dB, al variare della lunghezza del filtro.

Nonostante le caratteristiche non esaltanti nel dominio della frequenza, il filtro a media mobile presenta alcuni vantaggi rispetto ad altri tipi di filtro. Prima di tutto è semplice da calcolare e quindi da implementare anche quando le risorse di calcolo a disposizione sono particolarmente limitate. Si potrebbe dimostrare facilmente, inoltre, che la media mobile è la soluzione ottimale per attenuare il rumore casuale su un segnale preservando più possibile la pendenza dei fronti di salita e di discesa degli impulsi.

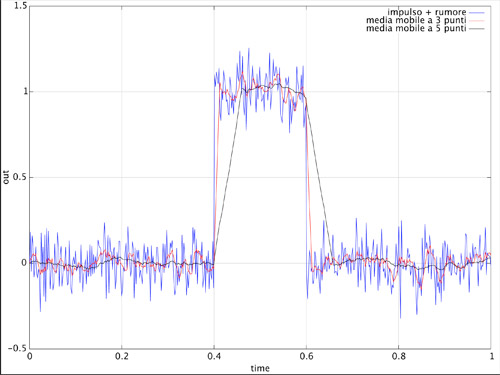
Figura 7: un impulso con rumore sovrapposto e il segnale filtrato con la media mobile.

Dal punto di vista della semplicità di calcolo del filtro a media mobile, un’interessante considerazione riguarda l’implementazione ricorsiva, tenendo presente che la media aritmetica di n valori è proporzionale alla loro somma. In corrispondenza di ciascun istante di campionamento, infatti, per ottenere il nuovo valore è sufficiente togliere alla somma precedente il valore più vecchio e aggiungere quello nuovo: una moltiplicazione, una sottrazione e una somma, oltre alla divisione per n, indipendentemente dalla lunghezza del filtro. Considerando, ad esempio, la media a cinque punti calcolata in precedenza, si può scrivere:

e quindi, per il campione successivo:

Avendo calcolato il campione precedente, però, si può utilizzare questo valore per calcolare il valore successivo:

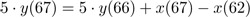
da cui:

Generalizzando, per qualunque valore di n:

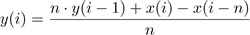
Occorre notare che quest’ultima implementazione della media mobile, pur essendo di fatto ricorsiva, non presenta le caratteristiche tipiche dei filtri ricorsivi in genere; mantiene, in particolare, la risposta all’impulso finita.

A questo punto lo spazio a disposizione è finito; non posso che ringraziare chi è arrivato a leggere fin qui, per l’attenzione che ha voluto dedicare a questo scritto. Nei prossimi numeri proseguirò la trattazione dell’argomento cercando di approfondire un poco i concetti alla base dei filtri FIR e IIR.