Analogico Digitale: andata e ritorno - 1

di Mario Di Cola e Marta Furlan

Da svariati anni il continuo e progressivo incedere delle tecnologie digitali nel campo dell’audio ha generato la comparsa di un sempre maggior numero di macchine che impiegano tali tecnologie per trasferire, trasformare, elaborare, registrare riprodurre, editare ecc. un segnale audio. Come è noto a quasi tutti oramai, per fare tutte queste cose “fiche” bisogna avere a disposizione il segnale audio inevitabilmente in formato numerico. Di pari passo credenze popolari ed equivoci di ogni tipo hanno preso posto nei discorsi e nei già tormentati sogni dei tecnici. Negli ultimi anni poi, nel settore del sound reinforcement, la tecnologia digitale sta tentando (riuscendoci) di impadronirsi proprio del ruolo più autorevole nella elaborazione del suono: il “mischiaggio” dei suoni. Le mixing console digitali, infatti, stanno prendendo a poco a poco il posto delle console analogiche in un sempre maggior numero di situazioni.
Vogliamo provare, con una breve serie di articoli, a fare un piccolo e timido tentativo di divulgare i concetti di base della conversione dei segnali. Ciò potrebbe essere molto utile per capire almeno in parte le idee che ci sono dietro e cosa accade all’interno delle macchine. Questi concetti saranno generici e quindi riguarderanno in generale la gran parte delle macchine di utilizzo comune. Molte macchine digitali, infatti, incorporano uno o più di questi dispositivi, così da permettere il contatto tra i due mondi: quello dei segnali analogici e quello dei segnali digitali.

Segnali analogici e digitali
Com’è noto, tranne in rari casi, ciò che riusciamo ad ottenere durante la ripresa di strumenti acustici o della voce, consiste in un piccolo segnale di tensione che varia proporzionalmente all’escursione della membrana di un microfono – ad esempio dinamico – col quale effettuiamo la ripresa.
Come tutti sanno, la variazione di pressione davanti alla membrana di un microfono mette la membrana stessa in movimento. Un apposito meccanismo di trasduzione (elettromeccanico o elettrostatico) converte questo movimento in una variazione di tensione all’uscita del microfono stesso.
Se rappresentassimo in funzione del tempo le variazioni della pressione davanti al microfono e la variazione della tensione del segnale in uscita su due grafici, scopriremmo che c’è diretta analogia tra i due. Innanzitutto il grafico della tensione presenta lo stesso andamento di quello della pressione, e in secondo luogo su di esso i valori di tensione  rilevati variano istante per istante con continuità, proprio come i valori di pressione.
Il segnale di tensione quindi, viene ad essere una particolare rappresentazione della pressione istante per istante e ne costituisce un “analogo” di tipo elettrico.

Anche se questo tipo rappresentazione è più naturale e più vicina (ovvero analoga: per questo parliamo di segnali analogici!) alla realtà, essa pone tuttavia una quantità enorme di problemi nel momento in cui volessimo realizzare sul segnale tutte quelle operazioni di cui sopra.
I segnali analogici possono infatti essere memorizzati grazie ad una “trasduzione” ulteriore: si può creare, ad esempio lungo un nastro magnetico, una variazione di campo magnetico che è anch’esso un analogo (magnetico questa volta) del segnale elettrico di partenza. Quando lo andiamo a rileggere, lo scorrere del nastro sulla testina produce sulla sua uscita di nuovo un segnale elettrico che è l’analogo di quello del campo magnetico memorizzato sul nastro e così via.
Se vogliamo rendere tutto questo più economico, riproducibile e se vogliamo davvero espandere le possibilità soprattutto dell’elaborazione, dobbiamo trovare una rappresentazione alternativa più efficiente ed efficace che consenta elaborazioni molto complesse e realizzabili con quelle macchine che sono diventate le protagoniste della nostra vita: i computer.
Per fare in modo di trattare i segnali con dei computer (o macchine simili a computer) è necessario dunque trovare una rappresentazione dei segnali compatibile con il formato dei loro dati.
Il primo scoglio da superare è costituito dal fatto che il segnale analogico è continuo, ovvero è definito per qualunque istante di tempo (l’asse dei tempi è formato da un numero infinito di punti): se noi volessimo memorizzare in un computer il valore del segnale per tutti gli istanti di tempo per i quali è definito, avremmo bisogno di infinite celle di memoria!
Ecco che la prima cosa da fare è “fotografare” il segnale solo in un numero finito di istanti di tempo, in modo che i suoi valori siano memorizzabili in una memoria fisica, e preoccupandoci di farlo “abbastanza spesso” in modo da non perdere quelle informazioni che ci servono per avere comunque un’idea precisa dell’andamento del segnale nel suo insieme. In più, come vedremo in seguito, se sono rispettati certi criteri molto precisi e restrittivi, la rappresentazione che otteniamo da questo fitto insieme di “fotografie” del segnale, è anche inequivocabile; cioè da essa si può ricostruire successivamente e senza alcun dubbio il segnale originario conoscendone anche con esattezza l’errore commesso nel processo. Dobbiamo in sostanza prendere dei “campioni significativi” del segnale. Il segnale da analogico diventa così discreto nel tempo: si compone di valori di tensione definiti solo per alcuni istanti di tempo. Abbiamo in altre parole campionato il segnale.

Tuttavia non possiamo ancora dare il segnale “in pasto” ai computer, in quanto quest’ultimo, com’è noto, accetta solo dati presentati in formato numerico binario e nelle celle di memoria di un computer i numeri sono espressi come sequenze di “0” e “1”. Che significa? Le celle di memoria RAM ad esempio non sono niente altro che piccoli circuiti basati su transistor in grado di mantenere all’uscita un valore di tensione che può essere “alto” o “basso”. Questi valori alti e/o bassi vengono letti dai circuiti di elaborazione rispettivamente come “1” e “0”. Ed è proprio su questa semplice convenzione che si basa peraltro la capacità del computer di eseguire elaborazioni matematiche sui dati memorizzati.
La seconda cosa da fare dunque è codificare i campioni del segnale in modo che risultino comprensibili al computer, in modo cioè che parlino “la stessa lingua”, trasformandoli in pure sequenze di bit in uscita al convertitore e rendendoli a tutti gli effetti digitali.

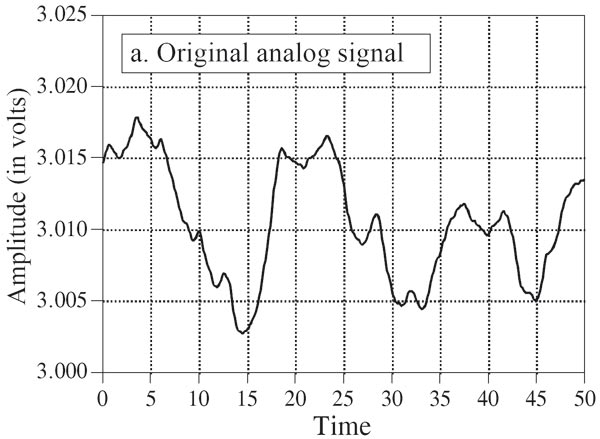
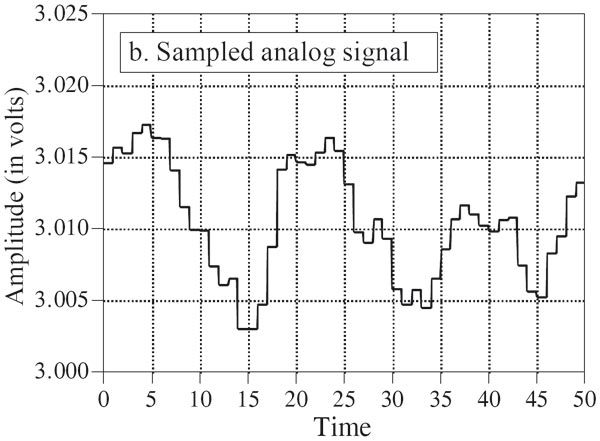
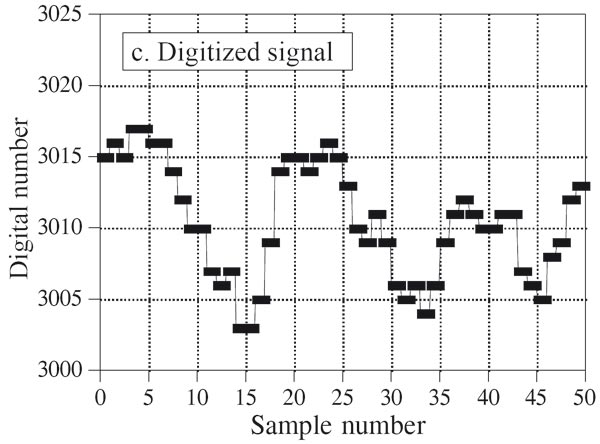
Un modello molto comodo
Questo modello “a due step” è utile per capire in modo intuitivo i passi necessari a trasformare il segnale di tensione e renderlo numerico. Non solo però, perché guarda caso all’interno dei convertitori in commercio le cose funzionano (per fortuna!) esattamente così! Un circuito dedicato (Sample & Hold) si occupa del campionamento e un circuito (che sarebbe il vero convertitore o ADC) traduce il valore in uscita dal S&H in formato numerico. Infatti, la questione a cui non abbiamo ancora accennato è che il segnale analogico originario non solo è continuo nel tempo ma è anche definito con continuità sulla scala dei valori di tensione. In sostanza, tra il minimo ed il massimo valore possibili nel particolare circuito analogico in cui transita, il segnale può assumere tutti gli infiniti possibili valori intermedi; e questo non è compatibile con la struttura reale dei computer. Il numero di celle della memoria non solo è finito (ed in ciascuna di esse mettiamo la fotografia di un istante solo, un campione, cioè) ma anche la dimensione di ciascuna di esse è finita e con questo dunque la risoluzione dei dati. Se abbiamo dunque reso discreto nel tempo un segnale, ora sarà necessario anche renderlo discreto nel valore del livello. Si dice che deve essere dunque quantizzato. Spieghiamo meglio: se abbiamo un segnale che può oscillare tra un minimo di -2 Volt ed un massimo di 2 Volt ed il nostro convertitore può riconoscere solo 1000 possibili livelli, così per sommi capi con un breve calcolo, abbiamo un’escursione di 4 V con 1000 scalini e quindi tra uno scalino e l’altro ci saranno 4 : 1000 = 0.004 V, cioè 4 mV. Se quindi in un certo istante il segnale vale 18 mV ed ipotizzando che il valori resi possibili dalla quantizzazione della scala siano 16 mV oppure 20 mV, il convertitore dovrà decidere (secondo un criterio) quale dei due valori assegnargli, consci che in ognuno dei casi il risultato è “falso” e contiene dunque un errore, che viene appunto detto errore di quantizzazione.

Nelle prossime puntate descriveremo meglio come avvengono le due fasi della conversione, capendo inoltre quali sono i parametri il cui controllo ne determina o meno la “buona riuscita”. Con  particolare attenzione alle tipiche tipologie di errore introdotte dall’operazione di conversione di un segnale, e lo faremo tenendo bene distinte le due fasi di cui sopra, in quanto ciascuna di esse introduce sul segnale analogico delle tipologie di errore assolutamente differenti.

Vedremo inoltre perché e in quali casi si può dire che “il digitale suona meglio”, ma allo stesso tempo cercheremo di sfatare importanti miti come “ho un convertitore a 24 bit anziché 16, dunque suona meglio”. Capiremo che una cosa è la risoluzione reale del convertitore di cui ci dotiamo, e una cosa è affermare che maggiore è la risoluzione e sempre e comunque meglio suona!
Ecco che la domanda: “Meglio convertitori a 8, 16, 20, o 24bit?” ha già una banale eppure importante risposta. È vero che più è alta la risoluzione di un convertitore e meglio è, in quanto esso è idealmente in grado di “rendere giustizia” al segnale analogico, di rilevarne cioè le più piccole variazioni. Ma se la circuiteria analogica che gli sta intorno non è in grado di fornire in pasto al convertitore segnali analogici altrettanto risoluti in quanto coperti da elevato rumore, a che ci serve tutto ciò?
Magari ne bastavano solo 16… ma buoni! E non è poi così raro trovare vecchie macchine a “soli” 16 bit magistralmente progettate che possono tuttora suonare meglio di molte macchine equipaggiate con convertitori a 24 bit, sì, ma poco più che giocattoli.

La prossima puntata in particolare sarà dedicata al Teorema del Campionamento, a come si può campionare un segnale in modo da non perdere informazioni, a cosa significa prendere i campioni significativi di un segnale ecc.
Vi anticipiamo però qualcosa: il teorema di cui sopra fornisce, a livello teorico, un importante criterio per essere sicuri di aver preso “abbastanza campioni” in modo da riuscire poi a ricostruire il segnale analogico a partire dai campioni stessi.
Il concetto di “abbastanza campioni” è strettamente legato alle componenti in frequenza del segnale analogico: più velocemente varia il segnale, più campioni dobbiamo prendere perché il segnale discreto sia “fedele” all’originale.

Questo è abbastanza intuitivo: pensate di fotografare un treno che viaggia con lo sfondo immobile della campagna. Potete fare 400 foto e osservandole ne concluderete che il treno viaggia, potete farne invece solo 2 e vi sarà chiaro di esservi persi qualcosa, ma vi sarà altrettanto chiaro che questo qualcosa non sarete più in grado di dire cos’era!
Invece, pensate di fotografare l’azione decisiva di una partita di calcio per un amico che non ha occasione di vederla: se vi sta simpatico fate una foto ogni 5 secondi, se invece gli volete male fotografate solo l’inizio e la fine, magari con la palla in rete! Credo proprio che il malcapitato avrà la sensazione di essersi perso qualcosa e non potrà, purtroppo per lui, ricostruire la scena.
E se volete fare proprio i bastardi, gli fate ugualmente una foto ogni 5 sec, ma alla fine gliene date una ogni tre, in modo da non fargli vedere l’ultimo passaggio ma solo la palla in rete. Lui penserà che il gol lo ha fatto Tizio anziché Caio e si presenterà gongolante al bar – poveraccio – pensando di aver vinto al Fantacalcio della giornata! Tutto questo perché voi gli avete fornito un “alias” della scena, cioè una “mascherata” della scena vera, qualcosa di estraneo che appare dall’interpretazione dei dati.

E con questo vi diamo appuntamento alla prossima puntata!

CLICCA QUI PER ACCEDERE ALLA SECONDA PARTE